4/6 to Percent: A Quick Guide

Converting Fractions to Percentages: A Simple Transformation

Converting fractions to percentages is a fundamental skill in mathematics, one that allows us to express values in a more intuitive and widely understood format. It’s a common practice across various fields, from statistics and finance to everyday life, where percentages offer a quick and clear way to convey proportions and probabilities.

Understanding the Fraction-to-Percentage Conversion

At its core, the process of converting a fraction to a percentage involves two simple steps:

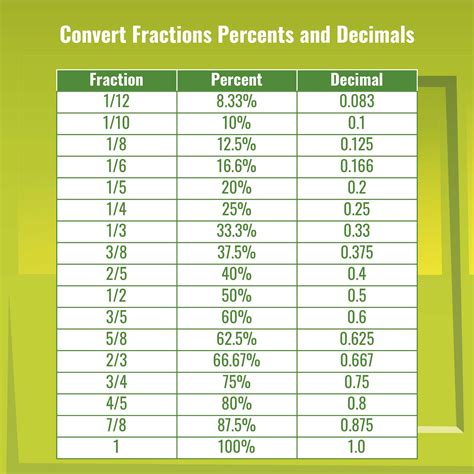
• Step 1: Understanding the Fraction - A fraction is a numerical value that represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). For instance, the fraction ⁴⁄₆ means four parts out of a total of six parts.

• Step 2: The Conversion Formula - To convert a fraction to a percentage, you multiply the fraction by 100 and then add the percentage sign (%). This is because a percentage is simply a fraction with a denominator of 100. So, the formula can be expressed as:

Fraction x 100 = Percentage (%)

For example, let’s convert the fraction ⁴⁄₆ to a percentage:

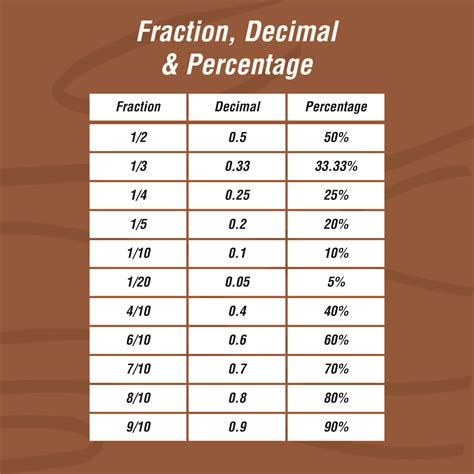
⁴⁄₆ x 100 = 66.67%

In this case, ⁴⁄₆ represents 66.67% of the whole.

Practical Applications

Converting fractions to percentages is a versatile skill with numerous real-world applications:

• Statistics and Data Analysis: When working with data sets, percentages offer a straightforward way to compare and interpret values, especially when presenting findings to a broader audience.

• Financial Transactions: In finance, percentages are commonly used to express interest rates, profit margins, and market share, providing a quick snapshot of financial health and performance.

• Everyday Life: From discounts and sales offers to nutrition labels and weather forecasts, percentages are ubiquitous in daily life, offering an accessible way to understand and communicate proportions.

Complex Scenarios and Advanced Techniques

While the basic formula works for most straightforward conversions, there are scenarios where more advanced techniques are required:

• Converting Mixed Fractions: A mixed fraction, like 2 ¹⁄₆, needs to be converted to an improper fraction (⁶⁄₆ + ¹⁄₆ = ⁷⁄₆) before applying the conversion formula.

• Dealing with Repeating Decimals: Some fractions, when converted to decimals, result in repeating sequences. In such cases, the decimal part can be rounded to a certain level of precision, depending on the context and required accuracy.

• Advanced Calculations: In certain fields like physics and engineering, more complex conversions may be required, involving fractions with large numerators and denominators or even fractions with variables.

Key Takeaway

Converting fractions to percentages is a fundamental skill with wide-ranging applications. While the basic formula is simple, understanding the underlying principles and being aware of advanced techniques can greatly enhance one’s ability to handle complex scenarios.

    <div class="faq-item">
        <div class="faq-question">
            <h3>Are there any limitations or potential errors when converting fractions to percentages?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>While the conversion formula is straightforward, it's essential to pay attention to precision and rounding. In some cases, especially with large fractions or those involving variables, rounding errors can occur, leading to slight discrepancies. Being mindful of the context and the required level of accuracy is crucial to avoid such errors.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>What is the practical significance of converting fractions to percentages in data analysis and research?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>In data analysis and research, converting fractions to percentages allows for a more intuitive and accessible representation of data. It facilitates easier comparison and interpretation, especially when presenting findings to a non-technical audience. Percentages provide a quick snapshot of proportions, making complex data more understandable and actionable.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>Can converting fractions to percentages help in decision-making processes?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>Absolutely! Converting fractions to percentages is a valuable tool in decision-making. It allows for a clear understanding of proportions, probabilities, and risks. For instance, in business, it can help assess market trends, customer preferences, or financial performance, leading to more informed and strategic decisions.</p>
        </div>
    </div>
</div>