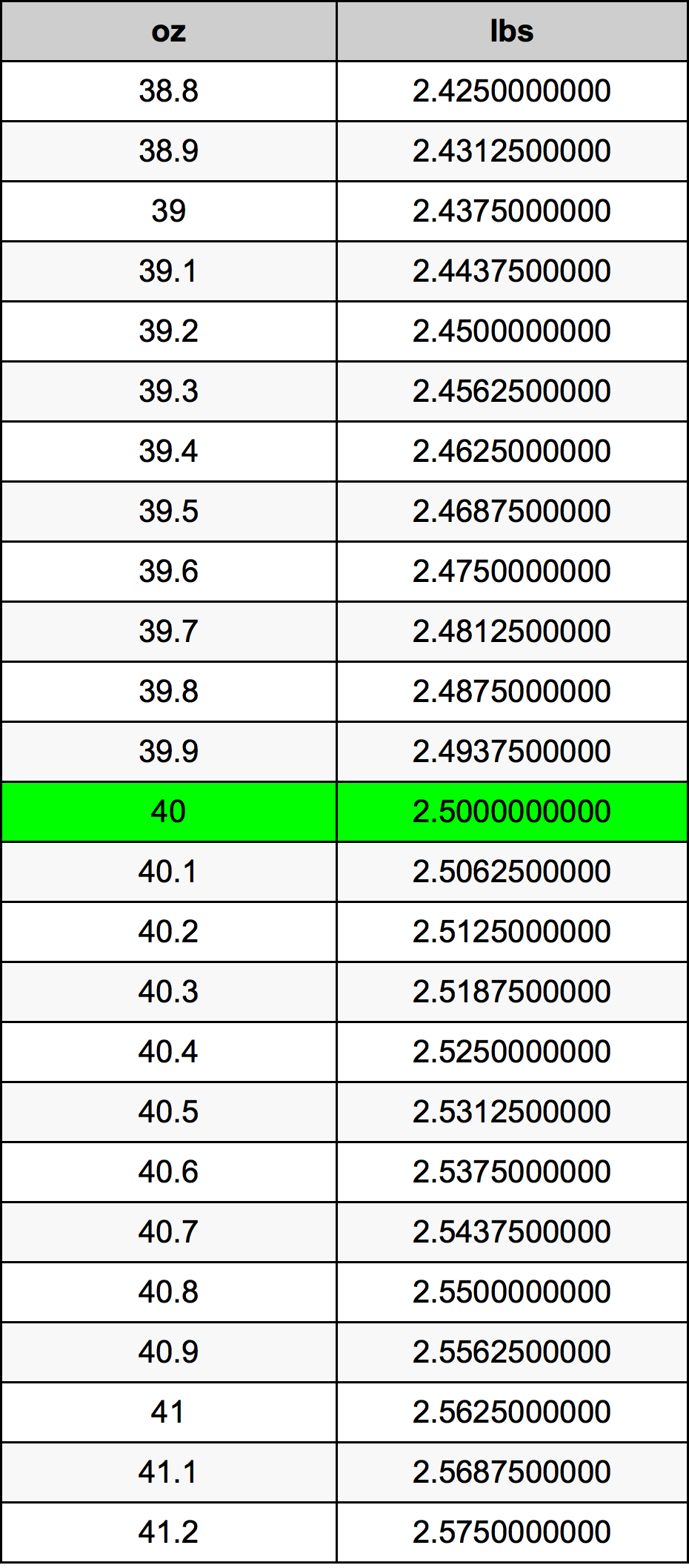
Unveiling the Mystery: 3 as a Fraction
Let’s dive into the fascinating world of fractions and explore the intriguing concept of representing the number 3 as a fraction. This seemingly simple task opens up a world of mathematical beauty and understanding. We’ll uncover the different forms this number can take and discover the insights it provides into the fundamental nature of fractions.
Understanding Fractions: A Brief Overview
At its core, a fraction is a way to represent a part of a whole. It is a numerical value that consists of two parts: the numerator (the top number) and the denominator (the bottom number). These two values work together to describe a specific portion or ratio. For instance, in the fraction 1⁄2, the numerator 1 tells us we have one part, and the denominator 2 informs us that this part is out of a total of two parts.
Fractions are an essential tool in mathematics, offering a precise way to express quantities that aren’t whole numbers. They find application in numerous fields, from engineering and physics to finance and daily life. For instance, when we talk about a recipe requiring 3⁄4 cups of milk, we’re using fractions to precisely define the quantity needed.
Representing 3 as a Fraction: A Multifaceted Approach
When we think of the number 3, we typically envision a whole number. But in the realm of fractions, 3 can be expressed in various ways, each offering a unique perspective. Here’s a look at some of these representations:
3 as a Simple Fraction: The most straightforward way to represent 3 as a fraction is simply 3⁄1. In this form, the numerator 3 indicates we have three parts, and the denominator 1 signifies that these parts make up the whole. It’s a simple and direct representation.
3 as a Complex Fraction: We can also express 3 as a complex fraction. This involves writing 3 as the numerator and a whole number as the denominator, creating a fraction within a fraction. For instance, 3⁄2 is a complex fraction, with 3 as the numerator and 2 as the denominator. This form is particularly useful when performing operations like division, as it can simplify the process.
3 as a Mixed Fraction: A mixed fraction combines a whole number and a proper fraction. In this case, 3 can be expressed as 3 0/1, where the whole number 3 is followed by a fraction with a numerator of 0 and a denominator of 1. This form is often used when dealing with measurements or quantities that involve both whole numbers and fractions.
3 as a Decimal Fraction: Fractions can also be expressed as decimals. To represent 3 as a decimal fraction, we simply write it as 3.0. This form is commonly used in scientific and technical fields, as decimals offer a more precise representation of numbers.
3 as a Percentage: Percentages are essentially another way to express fractions. To represent 3 as a percentage, we write it as 300%. In this form, the number 300 represents three out of every hundred parts, or 3⁄100. Percentages are often used in statistical analysis and financial calculations.
The Significance of Representing 3 as a Fraction
Why is it important to explore these different ways of representing 3 as a fraction? Each form provides a unique perspective on the number, offering insights into its properties and relationships with other numbers.
For instance, expressing 3 as a simple fraction (3⁄1) highlights its role as a whole number, emphasizing its completeness and unity. On the other hand, representing 3 as a complex fraction (e.g., 3⁄2) showcases its ability to be divided into parts, underscoring its potential for further analysis and manipulation.
The mixed fraction form (3 0/1) demonstrates how 3 can be both a whole number and a fraction, bridging the gap between these two types of numbers. This form is particularly useful when dealing with measurements or quantities that involve both types.
Expressing 3 as a decimal (3.0) or percentage (300%) offers a more precise and standardized representation, making it easier to compare and analyze data. These forms are essential in fields where precision and standardization are crucial, such as science, engineering, and finance.
Practical Applications and Real-World Examples
The ability to represent 3 as a fraction has numerous practical applications. Here are a few real-world examples:
Engineering and Construction: In construction, fractions are used to specify precise measurements. For instance, when calculating the amount of material needed for a project, fractions like 3⁄4 or 3 1⁄2 can be crucial to ensure accuracy.
Cooking and Baking: Recipes often require precise measurements, and fractions like 3⁄4 cups or 3 teaspoons are commonly used. Converting between different measurement systems (e.g., cups to grams) also involves fractions.
Financial Analysis: Fractions and percentages are essential in financial calculations. For instance, when calculating interest rates or analyzing investment returns, fractions like 3⁄100 (or 3%) can represent annual interest rates or returns.
Statistical Analysis: In statistics, fractions and percentages are used to represent proportions and probabilities. For example, if 3 out of every 10 people prefer a certain product, this can be expressed as 3⁄10 or 30%.
A Deeper Dive into Fraction Theory
Exploring the various ways to represent 3 as a fraction opens up a broader understanding of fraction theory. It showcases the flexibility and versatility of fractions as a mathematical tool.
Fractions allow us to break down numbers into their constituent parts, offering a deeper understanding of their properties and relationships. They enable us to analyze and manipulate numbers in ways that aren’t possible with whole numbers alone.
Furthermore, the ability to convert between different fraction forms (simple, complex, mixed, decimal, percentage) demonstrates the interconnectedness of mathematical concepts. It shows how different representations can be used interchangeably, depending on the context and the desired level of precision.
Conclusion: Unlocking the Beauty of Fractions
In conclusion, the seemingly simple task of representing 3 as a fraction reveals a rich and complex mathematical landscape. It highlights the power and versatility of fractions as a tool for understanding and manipulating numbers.
By exploring the different forms that 3 can take as a fraction, we gain a deeper appreciation for the beauty and utility of fractions in mathematics. They offer a window into the fundamental nature of numbers, providing insights that extend far beyond the simple representation of 3.
So, the next time you encounter the number 3, remember the myriad ways it can be expressed as a fraction, and appreciate the richness and depth that fractions bring to the world of mathematics.