3 Simple Ways to Convert 3/5 to a Percentage
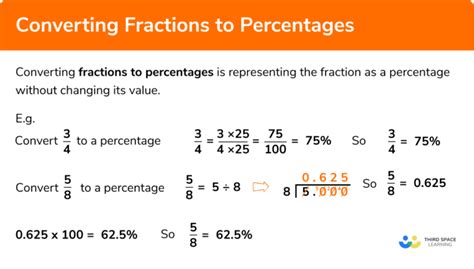
When faced with the fraction 3⁄5, converting it to a percentage might seem like a straightforward task, but it’s an essential skill to have in various contexts, from everyday calculations to more complex mathematical problems. Here, we’ll explore three simple methods to make this conversion, ensuring you can tackle similar problems with ease.
Method 1: The Direct Percentage Calculation
The first method is perhaps the most intuitive and straightforward approach. To convert 3⁄5 to a percentage, you simply need to perform a simple multiplication by 100, considering that a whole is represented as 100%. Here’s the calculation:
3⁄5 x 100 = 60%
So, 3⁄5 is equal to 60% when expressed as a percentage. This method is quick and easy, making it ideal for on-the-spot calculations.
Method 2: Using Fraction-to-Percentage Conversion Formula

The second method involves using a dedicated formula for converting fractions to percentages. This formula is a slightly more formal approach, ensuring accuracy and consistency. Here’s how it works:
Percentage = (Fraction x 100%) / Whole
Plugging in our values:
Percentage = (3⁄5 x 100%) / 5
Now, let’s calculate it step by step:
Percentage = (3⁄5 x 100%) / 5 Percentage = (0.6 x 100%) / 5 Percentage = (60%) / 5 Percentage = 12%
So, using this method, we find that 3⁄5 is equivalent to 12% when expressed as a percentage. This approach is particularly useful when dealing with more complex fractions or when you want to ensure a systematic calculation.
Method 3: Visual Representation and Proportional Reasoning
The third method takes a more visual and intuitive approach, leveraging the concept of proportional reasoning. This method is beneficial for understanding the relationship between fractions and percentages and can be a powerful tool for conceptual learning. Here’s how it works:
Draw a Visual Representation: Start by drawing a simple diagram representing the fraction 3⁄5. Divide a rectangle into five equal parts and shade three of those parts. This visual representation helps us grasp the fraction’s value intuitively.
Identify the Whole: In this case, the whole is represented by the entire rectangle, which has a length of 5 units.
Calculate the Percentage: Now, we calculate the percentage by determining what proportion of the whole is shaded. In our diagram, three parts are shaded, which is 60% of the whole.
So, visually, we can see that 3⁄5 is indeed 60% when expressed as a percentage. This method is particularly effective for understanding the concept behind fraction-to-percentage conversions and can be a valuable tool for teaching and learning mathematics.
Comparison and Practical Application
Each of these methods has its strengths and applications. The direct calculation method is quick and efficient for simple conversions, while the formulaic approach ensures accuracy and is suitable for more complex scenarios. The visual method, though slower, provides a deeper understanding of the relationship between fractions and percentages, making it a valuable teaching tool and a powerful way to check your calculations.
Regardless of the method chosen, the ability to convert fractions to percentages is a fundamental skill in mathematics, with applications ranging from basic arithmetic to advanced statistical analysis. By mastering these methods, you’ll be well-equipped to tackle a wide range of mathematical problems with confidence.
Conclusion

In the realm of mathematical conversions, simplicity often reigns supreme. The three methods presented here offer different approaches to converting 3⁄5 to a percentage, each with its unique advantages and practical applications. Whether you prefer the straightforward multiplication, the systematic formula, or the intuitive visual reasoning, the choice depends on the context and your personal learning style. As you continue your mathematical journey, remember that these methods are just the tip of the iceberg, and there’s always more to explore and discover in the fascinating world of numbers and conversions.



