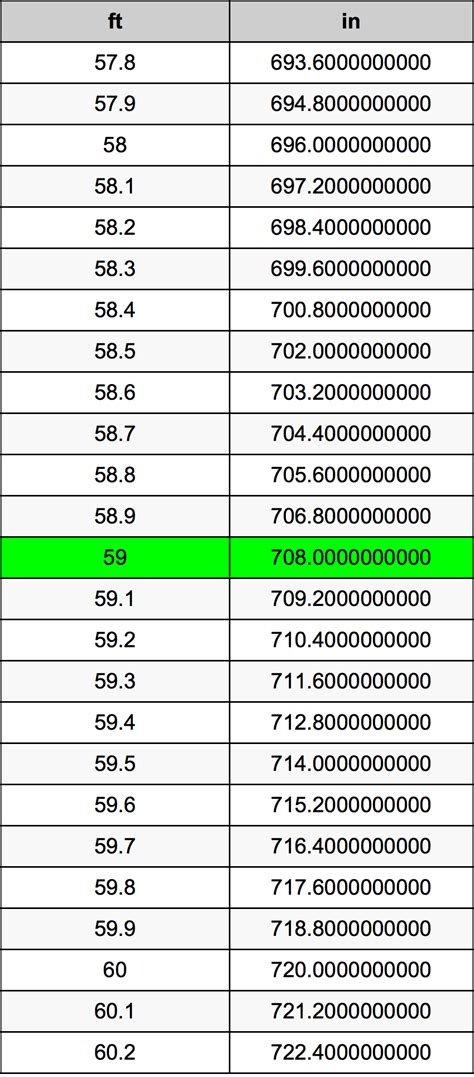
Unveiling the Mystery: 2 to the Power of Zero
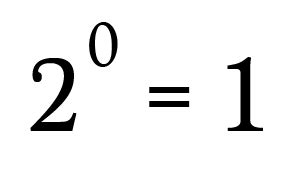
In the realm of mathematics, where numbers and operations intertwine to create a complex tapestry, one intriguing puzzle has long intrigued mathematicians and students alike: what is the value of 2 raised to the power of zero, or 2^0? At first glance, it might seem like a simple problem with an obvious answer, but as we delve deeper, we uncover a captivating journey through the fundamentals of exponential functions and the nuances of mathematical definitions. This exploration will not only shed light on the solution to this mystery but also highlight the elegance and depth of mathematical concepts that underpin our understanding of the world.
The Intuitive Approach: A Power of One?
Let’s begin with a straightforward interpretation. When we raise a number to a power, we’re essentially multiplying that number by itself a certain number of times. For instance, 2^2 means we multiply 2 by itself twice, resulting in 4. So, it’s natural to assume that 2^0 might signify zero multiplications of 2, leading us to conclude that 2^0 is simply 2. However, this intuitive approach, while seemingly logical, brushes over a crucial aspect of mathematical definitions.
Diving into Exponential Functions
Exponential functions are a fundamental concept in mathematics, with a wide range of applications across various fields. They describe situations where a quantity increases or decreases at a rate proportional to its current value. In the context of our 2^0 mystery, understanding the behavior of exponential functions is key.
Consider the general exponential function f(x) = a^x, where a is a positive real number and x can be any real number. The value of f(x) depends on the base a and the exponent x. When x is positive, we get a multiplied by itself x times, as mentioned earlier. For example, 2^3 = 2 \times 2 \times 2 = 8.
However, when x is zero, something intriguing happens. The function f(0) = a^0 no longer represents a simple multiplication. Instead, it introduces a unique case that requires a more nuanced understanding.
The Zero Exponent Conundrum
The concept of a zero exponent is not merely a mathematical curiosity; it has practical implications in various scientific and engineering applications. For instance, in physics, exponential functions describe the behavior of certain phenomena, such as the decay of radioactive isotopes or the growth of bacterial populations. In these contexts, understanding the behavior of a^0 is crucial for accurate predictions and modeling.
So, what happens when x is zero? Let’s explore some properties and definitions that shed light on this mystery:
- Identity Element: In mathematics, an identity element is a special value that, when combined with another value using a specific operation, leaves that value unchanged. For multiplication, the identity element is 1. Thus, a \times 1 = a for any a.
- Property of Exponents: One fundamental property of exponents states that a^1 = a for any a. This property is a direct consequence of the definition of exponents, where raising a number to the power of 1 signifies a single multiplication by that number.
- Definition of Zero Exponent: Extending this property, we define a^0 = 1 for any non-zero a. This definition ensures consistency with the identity element property and maintains the fundamental rules of exponents.
By defining a^0 as 1, we not only maintain the consistency of mathematical operations but also establish a solid foundation for more complex mathematical theories and applications.
Historical Perspective: A Journey Through Definitions
The definition of a^0 as 1 is not a recent invention but a result of centuries of mathematical exploration and refinement. Mathematicians, from ancient times to the present day, have grappled with the intricacies of exponential functions and their behavior.
In the ancient world, mathematicians like Euclid and Archimedes laid the foundations of mathematics, but the concept of exponential functions as we understand them today was yet to emerge. It was not until the 17th century that mathematicians like John Napier and René Descartes made significant contributions to the development of exponential and logarithmic functions.
During the Enlightenment era, mathematicians such as Leonhard Euler and Joseph-Louis Lagrange further refined these concepts, leading to the modern definition of exponential functions. Euler, in particular, played a pivotal role in establishing the connection between exponential functions and complex numbers, which laid the groundwork for many advanced mathematical theories.
Practical Applications: Unlocking Real-World Significance
The mystery of 2^0 might seem like a purely academic exercise, but its resolution has tangible implications in various fields. Let’s explore some practical scenarios where understanding the zero exponent is crucial:
- Computer Science: In computer programming, especially in low-level languages, the zero exponent is often used to represent the base case in recursive algorithms. Understanding the value of 2^0 is essential for correct program execution and error-free code.
- Engineering: Engineers often encounter exponential functions when modeling physical systems. For example, in electrical engineering, exponential functions describe the behavior of circuits with time-varying signals. Knowing the value of 2^0 ensures accurate calculations and predictions.
- Economics and Finance: Exponential functions are prevalent in economic models, especially those related to compound interest and population growth. Understanding the zero exponent is crucial for making accurate financial projections and predictions.
The Case for 2^0 = 1: A Unified Perspective
While the intuitive approach might suggest 2^0 = 2, a deeper examination of mathematical definitions and practical applications provides compelling evidence for the alternative conclusion: 2^0 = 1. This unified perspective reconciles the intuitive desire for consistency with the formal definitions and properties of exponents.
By defining 2^0 as 1, we not only maintain the consistency of mathematical operations but also open the door to a wealth of mathematical theories and applications. This definition is not merely a mathematical convenience but a fundamental building block that underpins advanced mathematical concepts and real-world applications.
Conclusion: Unveiling the Mystery, Embracing Consistency
In our journey to uncover the mystery of 2^0, we’ve explored the intuitive approach, delved into the intricacies of exponential functions, and examined the historical evolution of mathematical definitions. We’ve also highlighted the practical significance of this seemingly simple problem in various scientific and engineering domains.
As we conclude our exploration, we’re left with a profound appreciation for the elegance and depth of mathematical concepts. The resolution of the 2^0 mystery is not just about finding the “right” answer; it’s about understanding the principles that govern mathematical operations and their implications in the real world.
In the realm of mathematics, where precision and consistency are paramount, the definition of 2^0 as 1 emerges as the logical and consistent choice. This conclusion not only solves our initial puzzle but also serves as a reminder of the beauty and complexity that underlie the mathematical tapestry we weave.