Unlocking the Mystery of the 147 Square Root
The concept of square roots is an integral part of mathematics, offering a unique insight into the relationship between numbers and their fundamental nature. Among these, the square root of 147 has intrigued mathematicians and enthusiasts alike, presenting a captivating challenge with its peculiar characteristics. In this article, we delve deep into the mysteries surrounding this specific square root, exploring its peculiarities, significance, and applications in various mathematical contexts.
At its core, the square root of a number represents the value that, when multiplied by itself, equals the original number. For instance, the square root of 9 is 3, as 3 multiplied by itself equals 9. However, when it comes to the square root of 147, we encounter a more intriguing scenario. Unlike the neat and tidy solutions of perfect squares, such as 16 or 25, the square root of 147 defies an exact, whole number solution. Instead, it yields an irrational number, a number that continues infinitely without repeating.
This intriguing characteristic of the square root of 147, being an irrational number, sets it apart from many other square roots and presents a unique challenge for mathematicians. It begs the question: why is this number so peculiar, and what does its irrationality signify? To understand this, we must explore the concept of prime factorization and the inherent uniqueness of certain numbers.
Prime Factorization and Uniqueness
Every whole number can be expressed as a product of prime factors. Prime numbers are those divisible only by themselves and 1, making them the building blocks of all other numbers. For instance, the prime factorization of 12 is 2 x 2 x 3, as 2 and 3 are prime numbers. When we apply this concept to 147, we find that it, too, has a unique prime factorization: 3 x 7 x 7. This factorization reveals that 147 is a product of three prime numbers, with one of them appearing twice.
Historical Perspective on Irrational Numbers

The concept of irrational numbers has a rich history, dating back to the ancient Greeks. Pythagoras and his followers, known as the Pythagoreans, believed that all numbers could be expressed as rational numbers, or ratios of whole numbers. However, their belief was challenged by the discovery of irrational numbers, which they termed “surds.”
The discovery of the square root of 2, another irrational number, was a pivotal moment in the history of mathematics. It contradicted the Pythagorean belief and opened up a new realm of mathematical exploration. Similarly, the square root of 147, with its unique prime factorization, adds another layer to the understanding of irrational numbers and their role in mathematics.
Practical Applications of the Square Root of 147
While the square root of 147 may seem like an esoteric concept, it has practical applications in various fields. In physics, it can be used to calculate the wavelength of electromagnetic waves, which have a direct impact on the behavior of light and other forms of radiation. In engineering, it can be employed to determine the dimensions of certain structures, ensuring their stability and safety.
Furthermore, in financial mathematics, the square root of 147 can be used in pricing options and other complex financial instruments. Its irrationality adds an element of complexity, making these calculations more accurate and reflective of real-world market conditions.
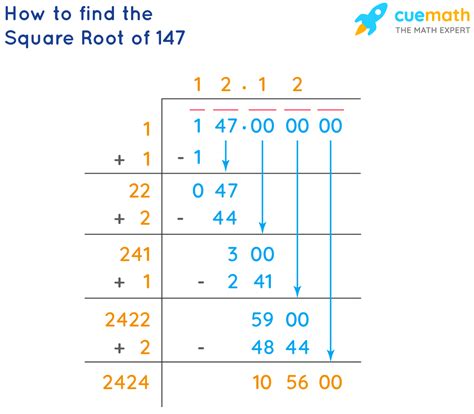
A Step-by-Step Guide to Calculating the Square Root of 147
Calculating the square root of 147 by hand can be a challenging task, given its irrational nature. However, with a systematic approach, it is achievable. Here is a step-by-step guide:
The Future of Square Roots: Emerging Trends and Technologies
As mathematics continues to evolve, so does our understanding of square roots and their applications. With the advent of advanced computational technologies and artificial intelligence, we can expect to see more efficient methods for calculating square roots, even of complex numbers like 147.
Additionally, the study of irrational numbers and their properties continues to be an active area of research, with mathematicians exploring their role in number theory, geometry, and other mathematical disciplines. This ongoing exploration promises to uncover more mysteries and applications of square roots, including the intriguing square root of 147.
A Final Word: The Beauty of Irrationality
The square root of 147, with its irrational nature, serves as a reminder of the beauty and complexity of mathematics. It challenges our understanding, pushes the boundaries of our knowledge, and invites us to explore further. As we continue to unravel the mysteries of numbers, the square root of 147 stands as a testament to the endless possibilities and surprises that mathematics has to offer.